 so I know some of you are disappointed ).
so I know some of you are disappointed ).So, I want to share with you some great things that made me love this science.
Let's talk about The Golden Ratio
The golden ratio, also known as the divine proportion, golden mean, or golden section, is an irrational mathematical constant, approximately 1.6180339887.
In order to describe the golden section, imagine a line that is one unit long. Then divide the line in two unequal segments, such that the shorter one equals x, the longer one equals (1 - x) and the ratio of the shorter segment to the longer one equals the ratio of the longer segment to the overall line; that is, x/(1 - x) = (1 - x)/1. That equality leads to ecuation: x^2-x-1=0. So, golden ratio is a solutino of this ecuation.
The Golden Section is a unique Ratio (or relationship between parts) that seems to be preferred by Nature as the best geometry for growth, energy conservation or elegance.
It was formally discovered by the Greeks and incorporated into their art and architecture, but it has been shown to occur even in prehistoric art, possibly as a function of Man's natural affinity for it's beauty.
Some Golden Geometry
1) The Golden Rectangle
A Golden Rectangle is a rectangle with proportions that are two consecutive numbers from the Fibonacci sequence.

The Golden Rectangle has been said to be one of the most visually satisfying of all
geometric forms. We can find many examples in art masterpieces such as in edifices of ancient Greece.
2) The Golden Triangle
If we rotate the shorter side through the base angle until it touches one of the legs, and then, from the endpoint, we draw a segment down to the opposite base vertex, the original isosceles triangle is split into two golden triangles. Aslo, we can find that the ratio of the area of the taller triangle to that of the smaller triangle is also 1.618. (=Phi)
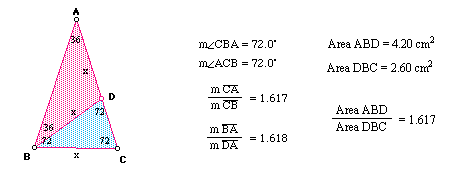
3) The Golden Spiral
The Golden Spiral above is created by making adjacent squares of Fibonacci dimensions and is based on the pattern of squares that can be constructed with the golden rectangle.
If you take one point, and then a second point one-quarter of a turn away from it, the second point is Phi times farther from the center than the first point. The spiral increases by a factor of Phi.
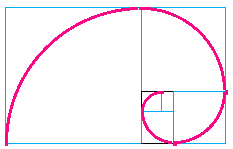
This shape is found in many shells, particularly the nautilus.

The Golden Section and The human body
The Golden Section, is manifested in the structure of the human body. If the length of the hand has the value of 1, for instance, then the combined length of hand + forearm has the approximate value of Phi. Similarly the proportion of upper arm to hand + forearm is in the same ratio of 1: Phi .

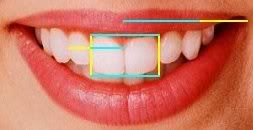
The human face abounds with examples of the Golden Section. The head forms a golden rectangle with the eyes at its midpoint.The mouth and nose are each placed at golden sections of the distance between the eyes and the bottom of the chin.Phi defines the dimensions of the human profile. Even when viewed from the side, the human head illustrates the Golden Proportion.

Phi proportions in teeth and lips
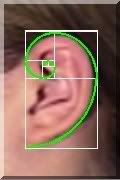
Phi Spiral of the Ear
The golden ratio in art and architecture
The appearance of this ratio in music, in patterns of human behavior, even in the proportion of the human body, all point to its universality as a principle of good structure and design.
Used in art, the golden ratio is the most mysterious of all compositional strategies. We know that by creating images based on this rectangle our art will be more likely to appeal to the human eye, but we don’t know why.
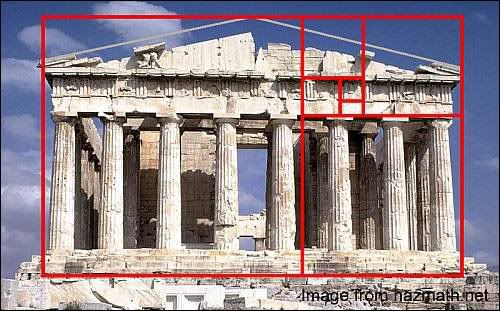
The ancient Greeks also used the golden ratio when building the Parthenon.
Artists throughout history, like Botticelli and Leonardo daVinci, have used the golden rectangle, or variations of it, as the basis for their compositions.
Here’s da Vinci’s painting, The Last Supper, with golden sections highlighted.

Golden rectangles are still the most visually pleasing rectangles known, and although they’re based on a mathematical ratio, you won’t need an iota of math to create one.
Mona-Risa by Leonardo Da Vinci

This picture includes lots of Golden Rectangles. In above figure, we can draw a rectangle whose base extends from the woman's right wrist to her left elbow and extend the rectangle vertically until it reaches the very top of her head. Then we will have a golden rectangle.
Also, if we draw squares inside this Golden Rectangle, we will discover that the edges of these new squares come to all the important focal points of the woman: her chin, her eye, her nose, and the upturned corner of her mysterious mouth.
It is believed that Leonardo, as a mathematician tried to incorporate of mathematics into art. This painting seems to be made purposefully line up with golden rectangle.
Good description of the Fibonacci Numbers with image examples of it in nature.
Luca Pacioli said: "Without mathematics there is no art"... Is obvious that he was right!
I want to thank my teacher Marinescu Daniela, Transilvania University of Brasov, Department of Computer Science, Brasov, Romania who inspired me. She presented the Golden Ratio to our last course(the goodbye course) and I think this was the only course that got my attention, that I understood from the beginning to the end

2 comments:
Alina, te imbratisez cu mare drag si cu multe emotii! Sunt raluk16. Ti-am vazut comentariul pe site-ul Inei si am intrat automat pe profilul tau sa vad ce mai faci! Ce super interesanta e postarea asta! De ce nu se fac oare toate cursurile din facultatile noastre asa de interesante?
Te pup!
wow, ralu! Ce ma bucur ca ne-am regasit! Mersi mult pentru comentariul tau! Asa e, facultatea ar fi de 10 ori mai interesanta daca profesorii si-ar da putin mai mult interesul. Ma bucur ca ti-a placut, te pup!
Post a Comment